Aujourd'hui, pas de Drupal ! Pour changer, je vais vous parler de Javascript et d'un petit effet de survol sympa avec lequel j'ai joué récemment. L'effet est visible en démonstration sur mon portfolio et est sûrement plus saisissant encore à la souris que sur mobile.
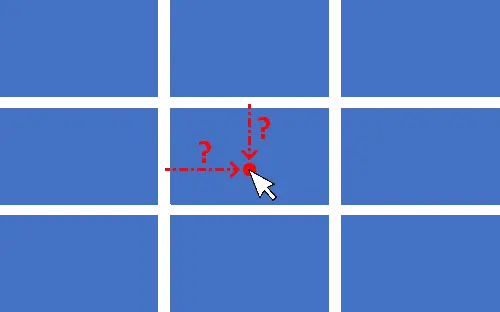
En anglais, il s'agit d'un direction-aware hover effect ce qui, je trouve, est très parlant mais difficile à traduire : "Effet de survol avec notion de direction" peut-être ? En d'autres mots, imaginez divers éléments (les vignettes de mon portfolio) : je veux un effet de survol qui apparaisse différemment suivant que je passe avec la souris sur mon élément en arrivant d'en haut, de la gauche, de la droite ou d'en bas. En bref, comme je le disais, un "effet de survol avec notion de direction" !
Le code en détail
Supposons le code HTML suivant :
Cliquez pour ouvrir/fermer ce bloc
<!doctype html>
<html lang="en">
<head>
<title>Direction-aware hover effect demo page</title>
<style>
.layout {
width: 1200px;
margin: 0 auto;
display: flex;
justify-content: space-between;
flex-wrap: wrap;
}
.hover {
background-color: lightblue;
position: relative;
display: flex;
flex: 1 1 30%;
margin: 1%;
height: 250px;
align-items: center;
justify-items: center;
}
.content {
flex: 1;
text-align: center;
}
.overlay {
position: absolute;
height: 100%;
width: 100%;
background-color: lightcoral;
opacity: 0;
}
</style>
<script>
/* Script will go here */
</script>
<style>
/* CSS will go here */
</style>
</head>
<body>
<div class="layout">
<div class="hover">
<div class="content">Item 1</div>
<div class="overlay"></div>
</div>
<div class="hover">
<div class="content">Item 2</div>
<div class="overlay"></div>
</div>
<div class="hover">
<div class="content">Item 3</div>
<div class="overlay"></div>
</div>
<div class="hover">
<div class="content">Item 4</div>
<div class="overlay">Info 4</div>
</div>
<div class="hover">
<div class="content">Item 5</div>
<div class="overlay"></div>
</div>
<div class="hover">
<div class="content">Item 6</div>
<div class="overlay"></div>
</div>
</div>
</body>
</html>Cette page HTML, volontairement basique dans un but d'exemple, présente une grille de 6 éléments à la manière de l'illustration du paragraphe précédent.
Un "overlay" recouvre chaque tuile d'un voile rouge sur un élément lui-même bleu : rien de bien palpitant.
Ajoutons le code javascript suivant :
document.addEventListener('DOMContentLoaded', function (event) {
// Loop over items (in a IE11 compatible way).
var items = document.getElementsByClassName('hover');
for (var i = 0; i < items.length; i++) {
// Loop over the registered event types.
['mouseenter', 'mouseleave'].forEach(function (eventname) {
// Add an eventListener of the given type for the current item element.
items[i].addEventListener(eventname, function (event) {
// Retrieve the direction of the enter/leave event.
var dir = getHoverDirection(event);
// Reset classes.
// > If support for IE11 is not needed.
// event.currentTarget.classList.remove('mouseenter', 'mouseleave', 'top', 'right', 'bottom', 'left');
// > If support for IE11 is needed.
event.currentTarget.classList.remove('mouseenter');
event.currentTarget.classList.remove('mouseleave');
event.currentTarget.classList.remove('top');
event.currentTarget.classList.remove('right');
event.currentTarget.classList.remove('bottom');
event.currentTarget.classList.remove('left');
// Add the event and direction classes.
// > If support for IE11 is not needed.
// event.currentTarget.classList.add(event.type, dir);
// > If support for IE11 is needed.
event.currentTarget.className += ' ' + event.type + ' ' + dir;
}, false);
});
}
});Ce code est assez verbeux du fait de la syntaxe javascript à l'ancienne et de la compatibilité IE11 que j'ai choisi de maintenir ici. Pour autant, il est extrêmement simple :
- Nous trouvons puis parcourons l'ensemble des éléments ayant la classe hover
- Pour chacun de ces éléments, deux listeners sont ajoutés permettant de réagir aux évènements suivants :
- L'utilisateur passe sa souris sur l'élément (ou touche l'élément sur mobile ou écran tactile)
- L'utilisateur sort sa souris de l'élément (ou touche l'écran en dehors de l'élément sur mobile ou écran tactile)
- Dans chacun des deux cas d'évènements, la procédure suivante est effectuée :
- L'élément est dépouillé de l'ensemble des classes possibles issues d'un évènement précédent
- Une classe du nom de l'évènement (mouseenter ou mouseleave) est ajoutée
- Une classe du nom de la direction d'entrée (top, right, bottom ou left) est ajoutée
Toute la magie réside dans la méthode getHoverDirection qui prend en paramètre l'évènement et qui renvoie le côté par lequel la souris entre sur l'élément sous la forme d'une chaîne de caractère valant top, right, bottom ou encore left selon le cas.
Voici le code de cette méthode :
/*
* Get the direction by which an element has been hovered.
*
* It is done by determining in which quadrant is the mouse
* inside the element when mouseenter/mouseleave event starts.
* This is done using trigonometry on the pointer position
* relative to the center of the element.
* @see https://freelance-drupal.com/node/79 for details
*
* @param event
* The event triggering the computation.
*
* @result string
* Can be 'top', 'right', 'bottom', 'left' depending on the situation.
*/
const getHoverDirection = function (event) {
var directions = ['top', 'right', 'bottom', 'left'];
var item = event.currentTarget;
// Width and height of current item.
var w = item.offsetWidth;
var h = item.offsetHeight;
// Calculate the x/y value of the pointer entering/exiting, relative to the center of the item.
// Scale (sort of normalize) the coordinate on smallest side to the scale of the longest.
var x = (event.clientX - item.getBoundingClientRect().left - (w / 2)) * (w > h ? (h / w) : 1);
var y = (event.clientY - item.getBoundingClientRect().top - (h / 2)) * (h > w ? (w / h) : 1);
// Calculate the angle to the center the pointer entered/exited
// and convert to clockwise format (top/right/bottom/left = 0/1/2/3).
var d = Math.round(Math.atan2(y, x) / 1.57079633 + 5) % 4;
return directions[d];
};Je pense que la plupart des développeurs se contenteront aisément de lire et copier ce code. Toutefois pour ceux qui désirent le comprendre plus en profondeur, le paragraphe "explications mathématiques" vous décrira en détail son fonctionnement. Le niveau de maths n'est vraiment pas un problème puisque la partie la plus complexe est un morceau de trigonométrie niveau 3ème.
Animation CSS
A ce stade, nous disposons désormais de la mécanique javascript pour compléter nos éléments hover par un duo de classe en fonction des interactions utilisateur :
- mouseenter ou mouseleave suivant que l'élément vienne d'être survolé ou quitté
- top, right, bottom ou left pour indiquer le bord par lequel l'évènement vient de se déclencher
Et c'est largement suffisant ! En effet ces deux seules classes nous permettent maintenant tout le CSS du monde pour définir différentes animations.
Voici la base du code CSS :
/* Hide overflowing HTML elements */
.hover {
overflow: hidden;
}
/*Animate overlay and move it 'above'*/
.hover .overlay {
transform: translate3d(-100%, 0, 0);
animation-duration: 0.5s;
animation-fill-mode: forwards;
animation-timing-function: cubic-bezier(0.25, 0.46, 0.45, 0.94);
}
/* Mouse enter event */
.hover.mouseenter.top .overlay {
animation-name: animation--enter-top;
}
.hover.mouseenter.right .overlay {
animation-name: animation--enter-right;
}
.hover.mouseenter.bottom .overlay {
animation-name: animation--enter-bottom;
}
.hover.mouseenter.left .overlay {
animation-name: animation--enter-left;
}
/* Mouse leave event */
.hover.mouseleave.top .overlay {
animation-name: animation--leave-top;
}
.hover.mouseleave.right .overlay {
animation-name: animation--leave-right;
}
.hover.mouseleave.bottom .overlay {
animation-name: animation--leave-bottom;
}
.hover.mouseleave.left .overlay {
animation-name: animation--leave-left;
}
Dans le détail :
- Tout élément qui sortirait du cadre de l'élément hover est rendu caché par l'usage de la propriété overflow configurée comme hidden.
- L'élément overlay est justement décalé de 100% de sa hauteur vers le haut. Il est donc entièrement au-dessus de l'élément hover, en "overflow" et donc non visible. Désormais, la position de base fait que le voile rouge est levé et l'élément est entièrement visible.
- Nous ajoutons également quelques réglages concernant les animations sur cet élément. Toute animation prendra 0.4s a s'effectuer. Une fois finie, l'overlay gardera l'affichage qu'il a à ce moment là, c'est à dire qu'il ne se réinitialise pas après l'animation. Enfin, le temps suivra une courbe de bézier bien particulière qui va faire que notre animation n'est pas tout à fait linéaire dans le temps. Par exemple une translation va accélérer pour finalement ralentir. Ce petit détail change tout !
- En dernier lieu, pour chaque type d'interaction, nous définissons une animation différente qu'il nous reste à définir.
Glissage
Un premier exemple d'interaction possible est celui que j'ai choisi dans mon portfolio: c'est un simple glissement de l'overlay.
/* Sliding animations ! */
@keyframes animation--enter-top {
0% { transform: translate3d(0, -100%, 0); }
100% { transform: none; }
}
@keyframes animation--enter-right {
0% { transform: translate3d(100%, 0, 0); }
100% { transform: none; }
}
@keyframes animation--enter-bottom {
0% { transform: translate3d(0, 100%, 0); }
100% { transform: none; }
}
@keyframes animation--enter-left {
0% { transform: translate3d(-100%, 0, 0); }
100% { transform: none; }
}
@keyframes animation--leave-top {
0% { transform: none; }
100% { transform: translate3d(0, -100%, 0); }
}
@keyframes animation--leave-right {
0% { transform: none; }
100% { transform: translate3d(100%, 0, 0); }
}
@keyframes animation--leave-bottom {
0% { transform: none; }
100% { transform: translate3d(0, 100%, 0); }
}
@keyframes animation--leave-left {
0% { transform: none; }
100% { transform: translate3d(-100%, 0, 0); }
}
Glissade-poussade !
Tout n'étant plus qu'une question de CSS, voici un autre exemple d'interaction possible, le glissade-poussade où l'overlay va pousser l'élément en lui-même.
Balançage
On continue avec les noms bizarres et démontrons ici un effet de bascule de l'overlay.
A vous la suite !
Il est temps de vous lancer : rotation de la tuile avec l'overlay sur l'autre face, zoom de l'overlay, transition en fondue, tout est possible !!
Explications mathématiques
A ce stade, la plupart des développeurs auront désormais soit compris le code ci-dessus, soit repris, adapté, modifié ce code à leur convenance. Toutefois, j'aimerais vous proposer une explication mathématique sur comment fonctionne la détection de la direction d'entrée. Ne prenez pas peur : nous pouvons tous faire semblant d'être très intelligent en faisant croire que l'on fait des maths de haut vol, mais nous sommes là sur une opération de trigonométrie d'un niveau de 3ème au maximum !
Au moment du survol de l'élément avec la souris (ou du toucher au doigt sur écran tactile), un événement est déclenché par Javascript. C'est cet évènement qui est passé à notre méthode getHoverDirection et de lui, nous allons obtenir les informations de position nécessaires à la suite.
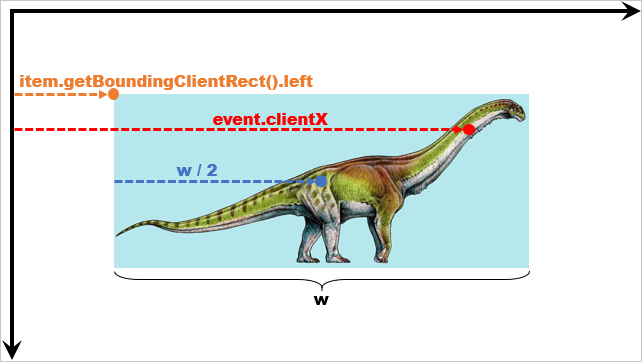
En premier lieu, nous extrayons de l'évènement l'élément dont le survol a déclenché l'opération. Cet élément a une position et une taille : en récupérer les dimensions hauteur, largeur est assez trivial. Pour ce qui est de la position, vous remarquerez deux choses :
- La position de l’élément est notée par son coin en haut à gauche, en orange dans l’illustration suivante. J’ai choisi ici de récupérer une position en pixel relative à l’écran, c’est-à-dire dont le point (0, 0) est celui en haut à gauche de l’écran. L’axe des y est donc inversé par rapport à l’habitude que nous avons de représenter nos axes. Plus y est grand, plus le point décrit est donc bas sur l’écran.
- La position de la souris ou du doigt au moment de l'évènement est notée par le point rouge. Contrairement à ce qui est couramment fait, nous ne récupérons pas la position eventX, eventY relative à la page, mais clientX, clientY relativement là aussi à l’écran. Nos deux positions sont donc dans le même repère spatial et pourront être comparées.
var x = (event.clientX - item.getBoundingClientRect().left - (w / 2))
Grâce aux positions des différents points remarquables de l'illustration précédente, nous pouvons calculer la position de l’évènement souris relativement au centre de l’élément.
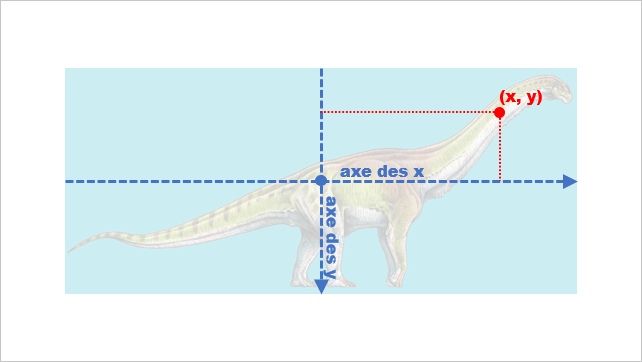
C’est donc un changement de repère que nous effectuons en faisant simplement une translation du centre du repère. La direction des axes ne changera pas, en particulier l’axe des ordonnées reste inversé. Désormais, un y négatif signifie que la souris se situe dans la moitié supérieure de l’élément, tandis qu'un y positif décrit une souris positionnée en moitié inférieure.
x = x * (w > h ? (h / w) : 1);
Pour la suite, nous aurons besoin d’inscrire l’image dans un cercle trigonométrique. Pour ce faire, nous devons effectuer une sorte de mise à l’échelle, ou encore de normalisation, de la position de notre souris dans un repère dont l’unité est la dimension la plus grande entre la hauteur et la largeur. Cela signifie que nous devons multiplier la position du côté le plus court par le ratio inverse des dimensions.
C’est une phrase bien compliquée pour dire que nous faisons « une règle de trois », dans la hauteur ou la largeur suivant que l’image est trop haute ou trop large.
Visuellement, cela signifie aussi que nos coordonnées de position sont désormais celles prises sur une image déformée pour être carrée (et donc tenir dans un cercle).
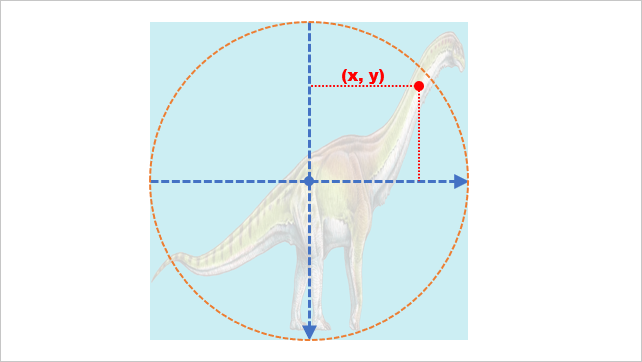
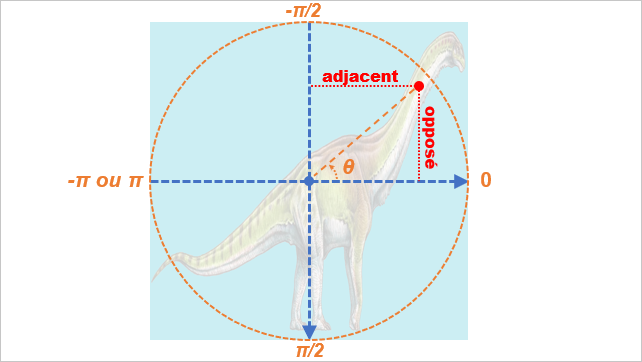
var theta = Math.atan2(y, x);
SOH CAH TOA !
Vous vous rappelez de ce moyen mnémotechnique ? TOA signifie Tangente de l'angle = Opposé sur Adjacent, et donc l'angle theta exprimé en radian est l'arctangente de la longueur opposée sur la longueur adjacente à cet angle dans le triangle trigonométrique.
Remarquez désormais que l'on s'exprime en radian et l'on peut ainsi connaître aisément la valeur de l'angle de quatre points remarquables qui vont nous intéresser par la suite.
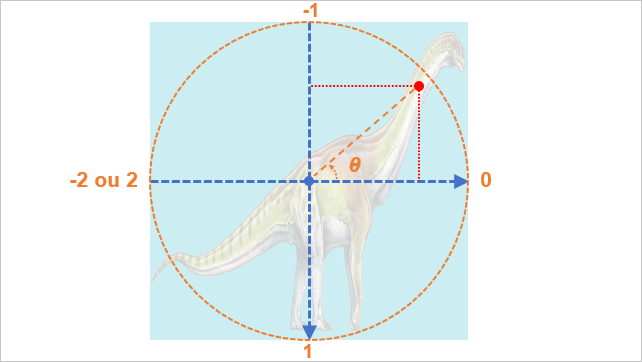
theta = thetha / 1.57079633);
Nous décidons désormais de diviser l'angle obtenu par PI/2 c'est à dire la moitié de PI ou encore environ 1.57079633...
Cela a pour effet de diminuer la valeur de cet angle. Nous pouvons également, du fait de la construction trigonométrique, déduire le quart (ou le cadran) dans lequel se trouve la souris, en fonction de la valeur de l'angle. Par exemple :
- Si notre souris se trouve comme sur le schéma, dans le quart en haut à droite de l'élément, alors la valeur de notre angle ainsi divisé et exprimé en radian est quelque part entre 0 et -1.
- Si notre souris se trouve dans le quart en haut à gauche, la valeur de notre angle est quelque part entre -1 et -2.
- Si notre souris se trouve dans le quart en bas à droite, notre angle vaut entre 0 et 1 radian
- Enfin si notre souris se trouve dans le quart en bas à gauche, notre angle vaut entre 1 et 2 radians.
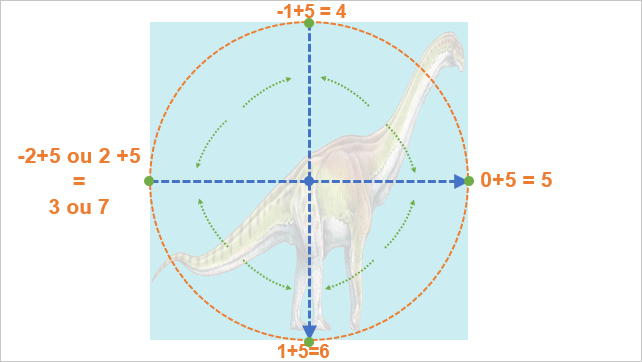
theta = theta + 5;
theta = Math.round(theta);
Voici deux opérations sur notre angle. Tout d'abord, nous ajoutons 5, ce qui permet d'obtenir des maximaux positifs en toutes circonstances, entre 1 et 5 suivant les cas (cf calcul en orange sur le schéma). Cela fonctionne pareil que l'opération précédente dont nous avons décrit la mécanique.
En second lieu, nous effectuons un arrondi à l'entier le plus proche de la valeur de l'angle. Visuellement sur le schéma, c'est l'opération notée en flèche verte : cela correspond à chercher quelle est la verticale ou l'horizontale la plus proche de l'endroit où se trouve la souris. L'angle est-il plus proche de la verticale ou de l'horizontale dans son cadran ?
Après cette opération, nous avons un angle qui correspond à l'un des quatre points (haut, droite, bas, gauche) des milieux des côtés de l'élément.
Comme chacun de ces points a une valeur différente, c'est gagné !
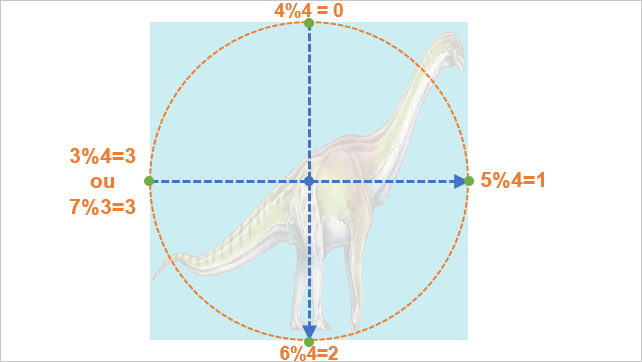
var d = theta % 4;
En dernier lieu, nous effectuons une opération dite de modulo sur la valeur. Ce modulo, c'est la recherche du reste de la division euclidienne. Autrement dit, 7 % 4 (7 modulo 4) vaut 3, car 7 divisé par 4 vaut 1 reste 3.
Cela nous permet d'avoir quatre cas distincts avec quatre valeurs : 0, 1, 2 ou 3. Ces valeurs pourront être utilisées par la suite comme index dans un tableau pour aller récupérer les classes correspondant aux directions.
var directions = ['top', 'right', 'bottom', 'left'];
return directions[d];
Le tour est joué ! En se servant des nombres obtenus comme d'indices dans un tableau, nous pouvons retourner la direction correcte selon la règle suivante :
- Si l'on a trouvé 0, c'est que l'on arrive du haut
- La valeur 1 indique une arrivée par la droite
- 2 pour le bas
- et enfin 3 si l'on vient de la gauche
Ajouter un commentaire